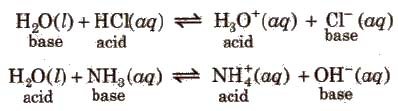L’acqua ha un comportamento anfotero infatti in presenza di un acido agisce da base secondo Bronsted-Lowry accettando uno ione H+ e in presenza di una base agisce da acido secondo Bronsted-Lowry donando uno ione H+:
Nell’acqua pura una molecola di acqua può agire come base accettando uno ione H+ da una seconda molecola di acqua che agisce da acido con formazione di uno ione H3O+ e di uno ione OH–.
Lo ione H3O+ è l’acido coniugato e lo ione OH– è la base coniugata dell’acqua e sono entrambi forti; non appena si formano essi reagiscono nuovamente per dare acqua secondo l’equilibrio:
2 H2O(l) ⇌ H3O+(aq) + OH–(aq)
Spesso questo equilibrio di autoionizzazione dell’acqua viene semplificato come:
H2O(l) ⇌ H+(aq) + OH–(aq)
La costante di equilibrio, indicata con il simbolo Kw, alla temperatura di 25°C ha un valore di 1.00 ∙ 10-14
Kw = [H3O+][ OH–] = 1.00 ∙ 10-14
Poiché il rapporto stechiometrico tra [H3O+] e [ OH–] è di 1:1 ciò implica che [H3O+]=[ OH–]. Detta x la concentrazione di H3O+ e quindi detta x la concentrazione di OH– si ha:
Kw = [H3O+][ OH–] = 1.00 ∙ 10-14 = (x)(x) = x2
pertanto a 25°C [H3O+]=[ OH–] = √ 1.00 ∙ 10-14 = 1.00 ∙ 10-7 M
A 25°C il pH dell’acqua così come il pOH assumono entrambi valore pari a 7.00.
I valori delle costanti di equilibrio rimangono costanti a temperatura costante e variando la temperatura varia il loro valore. Nello specifico stante l’importanza dell’acqua sono stati ottenuti i valori di Kw a diverse temperature come da tabella:
| T °C | Kw (mol2/dm3) |
| 0 | 1.14 ∙ 10-15 |
| 10 | 2.93 ∙ 10-15 |
| 20 | 6.81 ∙ 10-15 |
| 25 | 1.00 ∙ 10-14 |
| 30 | 1.47 ∙ 10-14 |
| 40 | 2.92 ∙ 10-14 |
| 50 | 5.48 ∙ 10-14 |
| 100 | 5.13 ∙ 10-13 |
Secondo i dati riportati in tabella quindi a 100 °C si ha:
Kw = 5.13 ∙ 10-13 = [H3O+][ OH–] = x2
Pertanto x = [H3O+]=[ OH–] = √ 5.13 ∙ 10-13 = 7.16 ∙ 10-7 M
Da cui pH = 6.14